Prev Next
Number Systems ( 21 to 25 ):
APTITUDE QUESTIONS (NUMBER SYSTEMS):
21. If x and y are positive integers such that (6x + 3y) is a multiple of 11, then which of the following will be divisible by 11?
A) 4x + 6y
B) 2x + 4y
C) 8x + 3y
D) 3x – 4y
E) None of these
View Answer
Answer: option (D)
Explanation:
By hit and trial, we put x = 5 and y = 1 so that (6x + 3y) = (6 * 5 + 3 * 1) = 33, which is divisible by 11
∴ (4x + 6y) = (4 * 5 + 6 * 1) = 26, which is not divisible by 11
(2x + 4y) = (2 * 5 + 4 * 1) = 14, which is not divisible by 11
(8x + 3y) = (8 * 5 + 3 * 1) = 43, which is not divisible by 11
(3x – 4y) = (3 * 5 – 4 * 1) = 11, which is divisible by 11
22. If 60% of 3/5 of a number is 36, then the number is:
A) 80
B) 100
C) 75
D) 90
E) None of these
View Answer
Answer: option (B)
Explanation:
Let the number be x.
Then, 60% of 3/5 of x = 36
- 60/100 * 3/5 * x = 36
- x = (36 * 25/9) = 100
∴ required number = 100
23. How many of the following numbers are divisible by 132?
264, 396, 462, 792, 968, 2178, 5184, 6336
A) 7
B) 5
C) 4
D) 8
E) None of these
View Answer
Answer: option (C)
Explanation:
132 = 4 * 3 * 11
264 = 4, 3, 11
396 = 4, 3, 11
792 = 11, 3, 4
462 = 11,3
968 = 11, 4
2178 = 11, 3
5184 = 3, 4
6336 = 11, 3, 4
Required Numbers are = 4
24. If n is natural number, then (6n2 + 6n) is always divisible by:
A) 6 only
B) 6 and 12 both
C) 12 only
D) 18 only
E) None of these
View Answer
Answer: option (B)
Explanation:
(6n2 + 6n) = 6n(n + 1), which is always divisible by 6 and 12 both, since n(n + 1) is always even.
25. What least number must be subtracted from 13601, so that the remainder is divisible by 87?
A) 33
B) 23
C) 29
D) 35
E) None of these
View Answer
Answer: option (C)
Explanation:
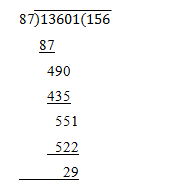
Required Number = 29
