Prev Next
Number Systems ( 11 to 15 ):
APTITUDE QUESTIONS (NUMBER SYSTEMS):
11. Which natural number is nearest to 9127 which is completely divisible by 88?
A) 9152
B) 9240
C) 9064
D) 9184
E) None of these
View Answer
Answer: option (A)
Explanation:
After dividing we get,
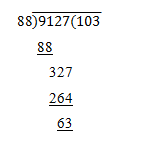
∴ required number = 9127 + (88-63) = 9127 + 25 = 9152
12. How many 3-digit numbers are completely divisible by 5?
A) 149
B) 180
C) 151
D) 166
E) None of these
View Answer
Answer: option (B)
Explanation:
3-digit numbers divisible by 6 are:
100, 105, 115,…., 995
This is an A.P. in which a = 100, d = 5 and l = 995
Let the number of terms be n. Then, tn = 995
∴ a +(n – 1)d = 995 => 100 + (n – 1) * 5 = 995
- 5 * (n – 1) = 895 => (n – 1) = 179 => n = 180
∴ Number of terms = 180
13. The sum of all two digit numbers divisible by 7 is
A) 1135
B) 1245
C) 1030
D) 945
E) None of these
View Answer
Answer: option (D)
Explanation:
Required numbers are 14, 21, 28, …., 98.
This is an A.P. in which a = 14, d = 7 and l = 98.
So, let the number of terms in it be n. Then,
tn = 98 => a + (n – 1)d = 98
- 14 + (n – 1) * 7 = 98 => (n – 1) * 7 = 84 => (n – 1) = 14 => n = 15
- Required sum = (n/2)(a + l) = 15/2(12+96)=(9*105) = 945
14. Which one of the following is the common factor of (4743 + 4343) and (4747 + 4347)?
A) (47 – 43)
B) (47 + 43)
C) (4743 + 4343)
D) (4747 + 4347)
E) None of these
View Answer
Answer: option (B)
Explanation:
If ‘n’ is odd, (xn + an) then it is always divisible by (x + a)
∴ each one of (4743 + 4343) and (4747 + 4347) is divisible by (47 + 43).
15. A number was divided successively in order by 4, 5, and 6. The remainders were respectively 2, 3 and 4. The number is:
A) 214
B) 476
C) 954
D) 1908
E) None of these
View Answer
Answer: option (A)
Explanation:
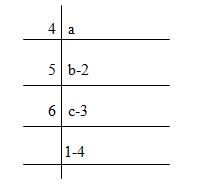
∴ c = 6 * 1 + 4 = 10
b = 5 * c + 3 = 5 * 10 + 3 = 53
a = 4 * b + 2 = 4 * 53 + 2 = 214
